Events are said to be independent when the outcome of one event does not affect the other.
On the other hand, two events are dependent when the occurrence or nonoccurrence of one event does affect the probability of the other event.
This is an important distinction, as we shall see.
When using the multiplication rule for independent events, sometimes we use the percent chance of success, other times we use the percent chance of failure. We must think about what we are trying to calculate when deciding which to use. If we want to calculate the probability that all the independent events will fail, then we would use the chances of failure. On the other hand, if we want the chance that all the independent events will succeed, then we use the chances of success. In a situation where we want the probability that one or more of the events will fail, then we would use one minus the multiplication of the chances of success (one minus the chance that all of the events will succeed will be the chance that one or more would fail).
Simple example: A software development project is going to proceed concurrently with the development of a new piece of hardware required to implement the software. Scheduled completion dates for both developments have been determined and a project plan has been created. Both projects can proceed independently until their respective completions (probably an unwarranted assumption, but I said this is a simple example!). Both projects must succeed in order for overall success to be achieved.
Using SLIM-Estimate, the probability of the software project being completed on the scheduled date has been estimated at 75%. Likewise, the probability of the hardware project being completed on the scheduled date has been estimated at 75%. Using these percentages, what is the probability that the project (both the hardware and software) will be implemented on time?
The multiplication rule says that .75 * .75 = 56% chance they will both complete on time. (6% chance that both will miss, 19% that the hardware only will miss, 19% that the software only will miss). On the other hand, if both the software and hardware projects were estimated and planned to a 50% solution, then the probability of both finishing on time is only .5 * .5 = .25, or 25%!
The assumption of independence is a very strong assumption. Quite often events have some dependencies on one another. This means that the multiplication rule doesn’t apply, and that the actual situation is more complex. Fortunately, we can use SLIM‐MasterPlan to help evaluate multiple estimates.
SLIM‐MasterPlan uses Monte Carlo analysis to give us insight into the effect of complex interrelationships between tasks has on the distribution of likely project completion times. Let’s look at an example.
This example program consists of 4 projects (or releases). Release 1 is set for low uncertainty and 2 through 4 are set to moderate uncertainty. This is a common situation, since we often have more knowledge about current work than we do about work farther in the future. To simplify things, the four releases are identical in size and productivity. Releases 2 through 4 have been set to start when the prior release is 50% complete.
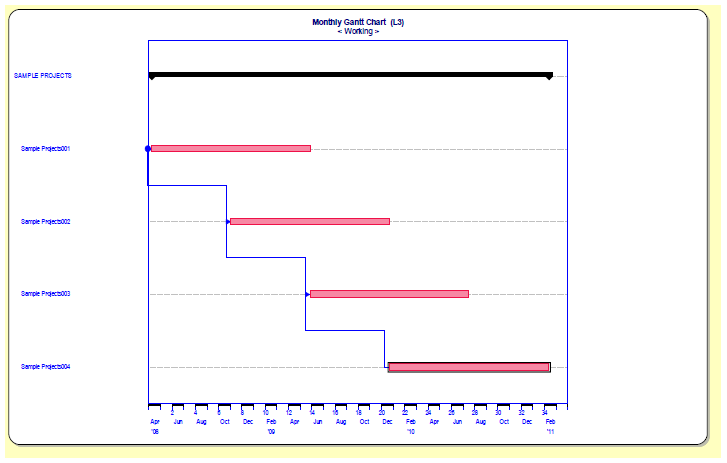
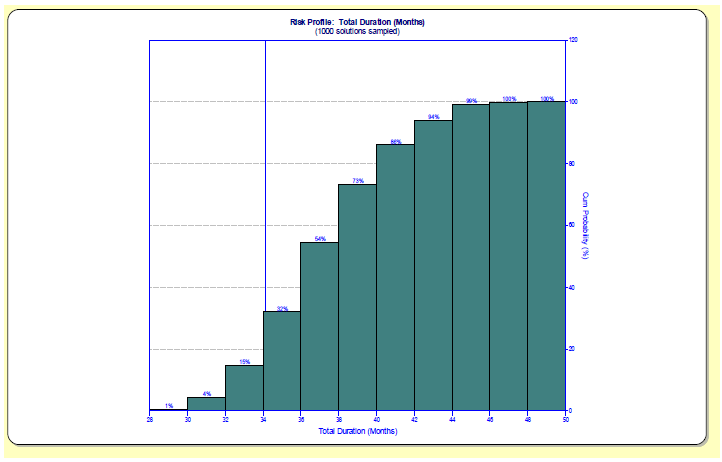
So, what is the probability that the program will complete on time? The answer is, about 20%. This is significantly less than the 50% that some people may have assumed when they created their program plan built upon 50% estimates for the individual releases. On the other hand, it is higher (whew!) than the 6% we would calculate if the four releases were truly independent and we needed all four to complete on time to be successful (.5 * .5 * .5 * .5 = .0625).
The following graph is the cumulative probability of program completion. The vertical line near 34 months represents the estimated completion date of release 4, the final release.
For programs with multiple projects or releases or iterations, let MasterPlan help you determine the likelihood of desired outcomes.
